数学で解説する複利の効果いつから実感？

はじめに
複利の効果が実感できる期間
まとめ

はじめに

以前、複利の効果について考察したのですが、ここでは複利の効果がいつえられるのか？数学で考察したいと思います。長年エンジニアをやってきた私ならではの切り口で、具体的な数式、数値を用いて分かりやすく解説したいと思います。以下の考察は、私独自の考察で、他では書かれていない内容かもしれませんが、数学的には正しいと思うので、内容には自信があります。数式には、でまかせや嘘はありません。ちょっと難しい内容かもしれませんが、お付き合い頂けると助かります。それでは始めます。

複利の効果が実感できる期間

結論

年利α％で、複利で運用したとすると、複利の効果が顕著に現れるのは、200/α 年後です。運用年数ｎとすると、n=200/αの前と後の二つの期間に分けて考えると以下のように言えます。

　n　<　200/α　の期間は準備期間
　200/α　<　n　の期間は爆増期間

複利の効果が感じられない理由

投資序盤は、複利の効果が感じられなく、爆増期間に突入するともの凄いスピードで資産が増えていきます。理由を説明します。

年利$\alpha\%でn年後の複利でお金がy倍となるyを求めると近似で以下の式であらわされる。$ $$y=\left(1+\frac{\alpha}{100}\right)^n\approx1+n\frac{\alpha}{100}+\frac{n\left(n-1\right)}{2}\left(\frac{\alpha}{100}\right)^2　\qquad\qquad\left(1\right)$$ 但し$n\frac{\alpha}{100}\ll1とする。$

(1)式の近似はここを参照。(1)式に運用するお金を掛け算するとn年後の残高が求まります。式のそれぞれについてみてみると、元本の項、単利の効果の項、複利の効果の項と分けることができ、それらの合計がn年後の残高を表します。

従って、元本、単利の効果、複利の効果のそれぞれどの項がどれだけ全体の残高に寄与しているのか？考察すれば複利の効果の真実がわかります。

年数ｎに対して、単利の効果の1乗の係数は α/100、複利の効果のn²に対する係数はα²/20000で単利の効果の係数より非常に小さい数字です。つまり複利の効果は単利の効果より係数が非常に小さいせいで、年数が経たないと効果が見えないが、2乗、３乗、、のべき乗の効果で年数が経つと爆増するという事がわかります。次に、元本、単利の効果、複利の効果が全体に与える寄与について具体例で計算します。

単利の効果と複利の効果のグラフ交点と複利の効果が得られるまでの期間

年利10%で計算し、excelでグラフを書いてみました。元本、単利、複利の合計を総合(元本+単利+複利)として計算しています。単利の効果は直線、複利の効果は放物線なので、単利と複利の交点を過ぎると、複利の効果がメインとなり、放物線を描きながら爆発的に増加するのがわかります。

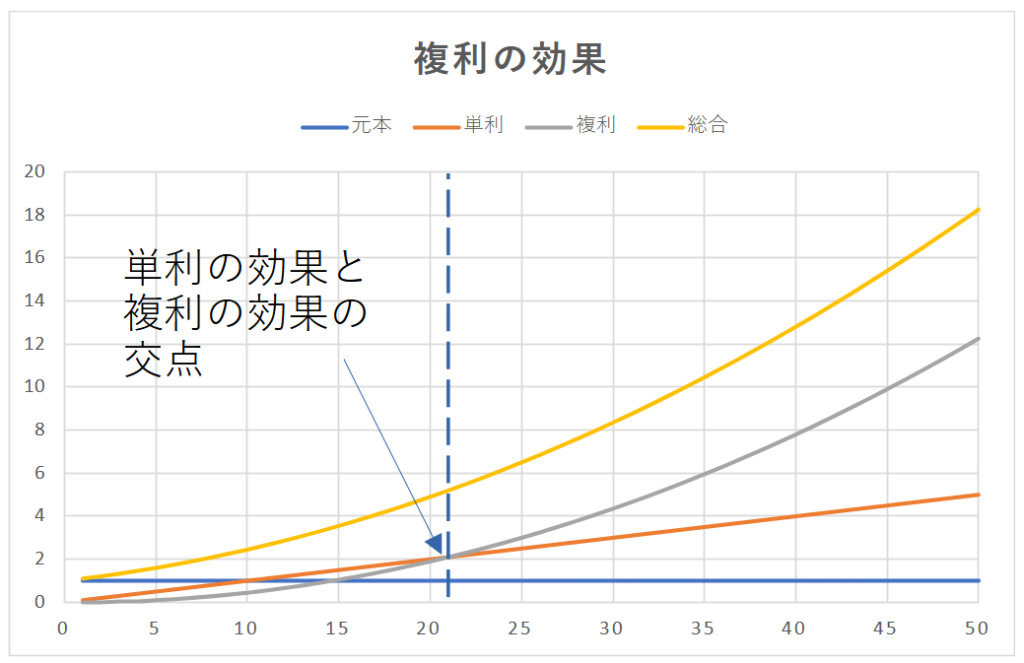
この交点を導出すると、運用利回りα[%]とすると近似で200/α。交点を過ぎると複利の効果が支配的になるので、200/α　より前は準備期間、後は爆増期間とわけることができます。

元本、単利の効果、複利の効果それぞれの寄与

運用利回り10%の時、運用残高に対して、元本、単利の効果、複利の効果の割合をそれぞれ計算してみました。

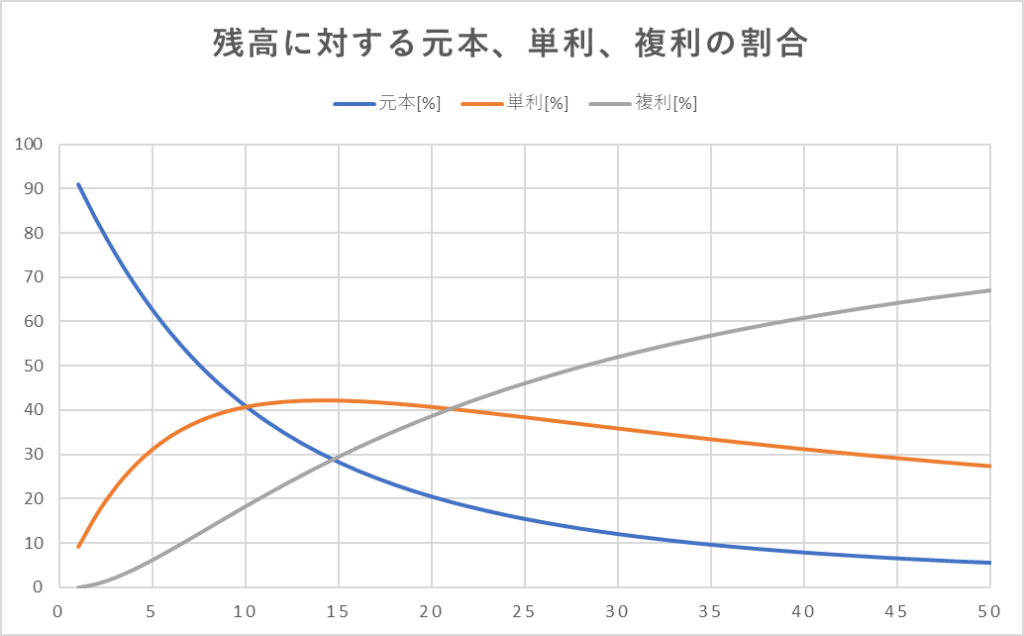
運用利回り10%の場合、最初は元本が100%で、初期は単利の効果の割合が増加し、単利の効果と複利の効果の交点を過ぎてから複利の効果が支配的になるのがわかります。

複利の効果がいつ？を計算すると、200/αなので運用利回りが　5%だと40年、６％だと33年、７％だと28年、10％だと20年、いずれも長いですが、実現不可能な期間ではありません。以上の考察からも、なるだけ早い段階で投資を始めて、なるだけ高利回りで、長期間複利で運用することが重要です。

複利の効果があるのかないのか？わかりにくいのは、理由は簡単で、複利の効果の係数が非常に小さい為、初期の頃は元本、単利の効果が支配的で、複利の効果が殆ど見えない。しかし、年数が経って、複利の効果が単利の効果を逆転すると、2乗、3乗、4乗とべき乗の項が支配的になり爆発的に増加するようになるからです。長く運用し続けないと見えないというのが理由です。